How to Use Standard Deviation to Describe Data

The higher deviation the more differences there are in the data set. And we can agree that the term we just derived accurately describes the deviation of each data point from the mean.

Empirical Rule Definition Formula And Uses Statistics By Jim Normal Distribution Standard Deviation Rules

More precisely it is a measure of the average distance between the values of the data in the set and the mean.

. Smaller values indicate that the data points cluster closer to the meanthe values in the dataset are relatively consistent. The standard deviation of a data set describes the difference between the data in the set and their mean. The simpliest interpretation could be.

The formula for standard deviation takes into account the mean of the data set by calculating the square difference between each data point and the mean. Just like the range the larger the difference between the highest and lowest values the greater the deviation and the higher the variability. A high standard deviation indicates that the data points are spread out over a large range of values.

It is rarely non-zero. In any distribution theoretically 9973 of values will be within -3 standard deviations of the mean. So the standard deviation of 17 is the square root of the average.

0 is the smallest value of standard deviation since it cannot be negative. And that is how we arrive at the formula for standard deviation. How does the mean and standard deviation describe data.

The mean and median are 1029 and 2 respectively for the original data with a standard deviation of 2022. The Standard Deviation of a set of data describes the amount of variation in the data set by measuring and essentially averaging how much each value in the data set varies from the calculated mean. The standard deviation is the average amount of variability in your data set.

For our data the deviation is. About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy Safety How YouTube works Test new features Press Copyright Contact us Creators. The standard deviation measures how concentrated the data are around the mean.

The more concentrated the smaller the standard. It represents the typical distance between each data point and the mean. The overall range of data is 9 - 1 8.

Standard deviation denoted by the symbol σ describes the square root of the mean of the squares of all the values of a series derived from the arithmetic mean which is also called the root-mean-square deviation. That is standard deviation tells us how data points are spread out around the mean. In the second histogram the overall range is 7 - 3 4.

The standard deviation s is the most common measure of dispersion. In fact as far as I know the only possibility for a data set to have zero deviation is when it contains only the same numbers. In the first histogram the largest value is 9 while the smallest value is 1.

The standard deviation is a measurement in reference to the mean that means. The standard deviation is used in conjunction with the mean to summarise continuous data not categorical data. The standard deviation of 17 shows how much dispersion there is from the mean wage.

Basically a small standard deviation means that the values in a statistical data set are close to the mean or average of the data set and a large standard deviation means that the values in the data set are farther away from the mean. It is a measure of how far each observed value in the data set is from the mean. A low standard deviation indicates that the data points tend to be very close to the mean.

Subtract the mean x from each value. Determine the mean the average of all the numbers by adding up all the data pieces xi and dividing by the number of pieces of data n. When the elements in a series are more isolated from the mean then the standard.

In normal distributions a high standard deviation means that values are generally far from the mean while a low standard deviation indicates that values are clustered close to the mean. At its most basic level the standard deviation tells us how spread out the data values are in a dataset. To illustrate this consider the following three datasets along with their corresponding standard deviations.

The formula for standard deviation depends on whether you are analyzing population data in which case it is called σ or. Standard deviation is a number that tells us about the variability of values in a data set. Standard deviation Square root of Sum of squared errors Total number of data points Also written as.

5 5 5 standard deviation 0 no spread at all 3 5 7 standard deviation 163 some spread 1 5 99 standard deviation 4528 a lot of spread. The data are plotted in Figure 22 which shows that the outlier does not appear so extreme in the logged data. To begin to understand what a standard deviation is consider the two histograms.

On a side note your deviations should always add up to zero. Up to 8 cash back We generally use s to represent deviation. It tells you on average how far each score lies from the mean.

Histogram 1 has more variation than Histogram 2. Where the mean is bigger than the median the distribution is positively skewed. Show activity on this post.

The standard deviation SD is a single number that summarizes the variability in a dataset. Square each of those differences. I would say that this suggests that wages are very spread out.

Use the standard deviation to determine how spread out the data are from the mean. In addition the standard deviation like the mean is normally only appropriate when the continuous data is not significantly skewed or has outliers. Precisely the standard deviation is the square root of the variance which is the average of the squared differences from the mean.

Standard deviation tells you how spread out or dispersed the data is in the data set. A large standard deviation indicates that the data points are far from the mean and a small standard deviation indicates that they are clustered closely around the mean. A higher standard deviation value indicates greater spread in the data.

Conversely higher values signify that the values.

Standard Deviation Homework Teaching Resources Standard Deviation Math Formulas Probability Worksheets

Learn How To Calculate Standard Deviation Standard Deviation Math Work Education Math

Process Capability And Non Normal Data Process Capability Data Standard Deviation

Formulas To Calculate Sample Standard Deviation Http Ncalculators Com Statistics Mean Standard Deviation Standard Deviation Learning Math Online Calculator

Chebyshev S Theorem In 2022 Theorems Standard Deviation Mathematics

Pin On Https Www Altdatum Com

Calculating Standard Deviation Data Science Learning Math Methods Physics And Mathematics

How To Calculate A Sample Standard Deviation Statistics Math Studying Math Standard Deviation

Range Different Between Higher Or Lower Scores In A Distribution Standard Deviation Square Root Of Ave Data Science Learning Statistics Math Central Tendency

The Standard Deviation Formula For A Sample Statistics Math Standard Deviation Descriptive

Read The Full Article Https 365datascience Com Coefficient Variation Variance Standard Deviation Watc Standard Deviation Data Science Science Blog

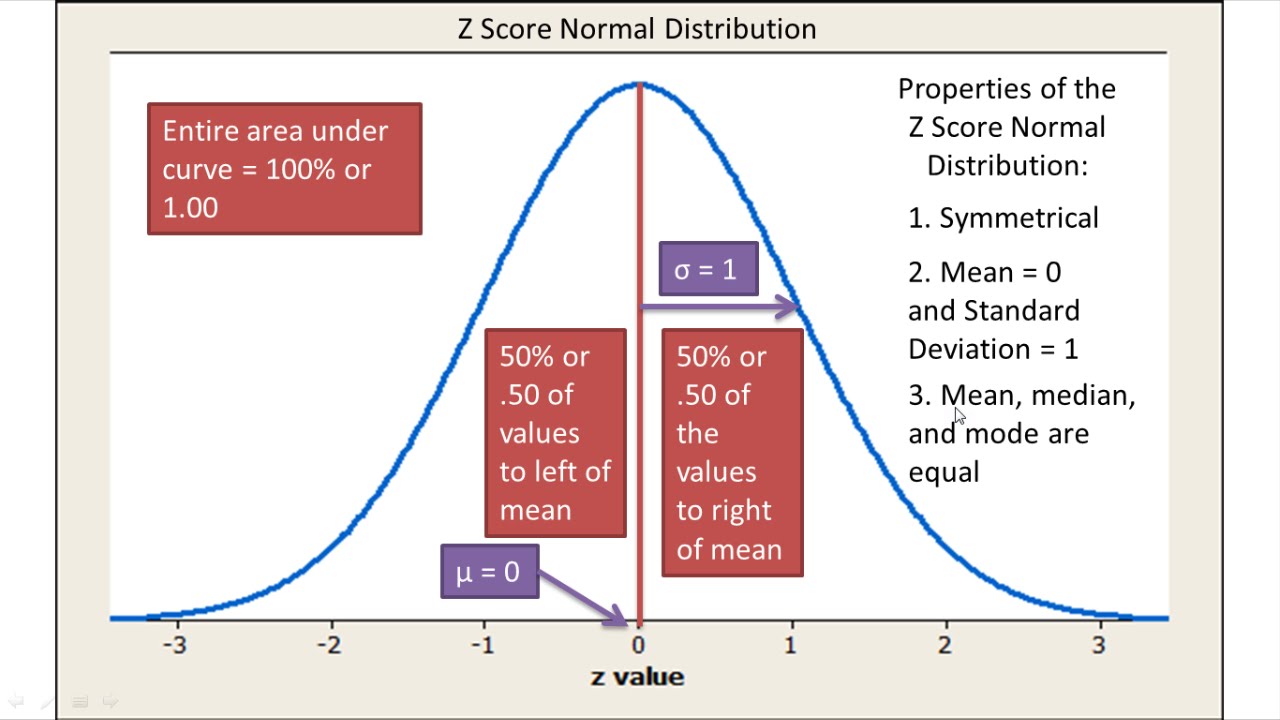
Normal Distribution And Z Scores Explained Introductory Statistics Statistics Math Statistics Notes Normal Distribution

Standard Deviation Approximately 68 Of All Observations From Repeated Samples Would Fall Within One Standard Devi Statistics Math Math Resources Medical Math

The Empirical Rule When A Population Has A Histogram That Is Approximately Bell Shaped Then Approximat Math Methods Standard Deviation How To Memorize Things